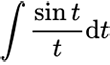欢迎来到中文数学 Wiki
你可以在这里来得知这个 wiki 如何运作的, 同时还需要留意一下社区规定, 也可以询问任意一名管理员获得你想要的帮助.
特别提醒: 如果你遇到网站加载速度问题, 公式以及图片显示问题请参见这里的说明.
以下是目前各社区内着重发展学科的进度表, 欢迎大家加入了解!
学科
进度
时期
状态
中学数学主题
初中数学
-
弧
弦
圆周角
圆心角
相交弦定理
平移
-
轴对称
中心对称
旋转
投影
三视图
解析几何
-
高中数学
空间几何
-
空间几何体及其表面积体积
-
柱体
锥体
台体
球体
射影
-
平行投影
中心投影
三视图
平面
-
空间中线面关系
空间中面面关系
空间中线线关系
空间中的度量性质(距离、角度)
-
空间向量基本定理
向量法研究空间几何
解析几何
更深的层次
数
学分析
mathematical analysis
数学分析是近代分析数学的基础,现行的理论源于近代 Cauchy, Riemann, Weierstrass 等人建立的极限论、积分和级数理论基础,该学科主要研究实变量函数(尤其是连续实函数)的微分积分性质,以及函数项级数的性质,多元函数主要关注各种物理中常用的微分定理和积分公式。后继课程有实分析以及复分析等等。
学科编码:11034,隶属于数学分析
实
变函数论
real analysis
学科编码:1104110,隶属于函数论
单
复变函数论
complex analysis
单复变函数论主要研究自变量为单个复数的函数的性质,因其关注的函数多是性质较好的解析函数,故该学科又称解析函数论,该学科的立足点可以从解析函数的微分理论、积分理论以及级数理论三方面进行,解析函数的微分理论引出所谓 Cauchy-Riemann 方程,而积分更像是二元复值实函数的第二类曲线积分,有著名的 Cauchy 积分公式,级数理论主要由 Weierstrass 建立,有著名的 Laurent 展开,此外对于复变函数的研究还有几何性质方面,由 Riemann 建立。先修课程为数学分析,后继课程有多复变函数论等。
学科编码:1104120,隶属于函数论
函
数逼近论
function approximation theory
函数逼近论主要研究函数的级数展开、渐近展开和数值计算,主要结果有插值问题(特别是多项式插值用于拟合函数或进行数值计算)、数值积分(著名结果有 Newton-Cotes 公式和 Romberg 算法)、函数逼近(最佳一致逼近和最佳平方逼近问题)和渐近展开理论。先修课程为数学分析。
学科编码:1104140,隶属于函数论
特
殊函数论
special function theory
特殊函数论主要研究在数学和物理中应用广泛的各种特殊函数(大部分是超越函数),这些函数有的借助级数定义,有的是某些特定问题的抽象化(如正弦积分函数等),有的是高阶(特别是二阶)常微分方程的解(这类函数众多),特殊函数论的众多公式经过众多数学物理学家的研究得到。系统学习特殊函数论的先修课程为数学分析,复变函数以及常微分方程等。
学科编码:1104170,隶属于函数论
主要
页面
页面
常
微分方程
ordinary differential equation
常微分方程简称 ODE, 含有未知的一元函数和未知函数各阶导数的方程称为常微分方程,对常微分方程的研究主要有定量研究(直接求解,这类方程十分稀少)、定性研究(主要研究方程的奇点和稳定性问题)以及数值方法(用数值方法求出特定初值问题对应的解)。
学科编码:11044,隶属于常微分方程
偏
微分方程
partial differential equation
偏微分方程简称 PDE, 含有未知的多元函数和未知函数各阶偏导数的方程称为偏微分方程,因其背景很多方程都源于物理学,故又称数学物理方程。主要研究椭圆的、双曲的以及抛物的偏微分方程,进一步的应用是动力系统。
学科编码:11047,隶属于偏微分方程
主要
页面
页面
泛
函分析
functional analysis
泛函分析是从代数结构的角度研究实变量的函数的学科,属于软分析(实变函数属于硬分析)。主要主题有线性算子理论、变分法、拓扑线性空间、希尔伯特空间、巴拿赫空间、算子代数以及测度与积分理论等等。
学科编码:11057,隶属于泛函分析
主要
页面
页面
线
性代数
Linear Algebra
线性代数是研究由通常的二维或三维向量空间抽象出来的代数结构——有限维线性空间的学科,为此引入了矩阵、行列式和向量组的相关理论,在研究线性空间的变换性质(映射性质)的过程中又引入了特征子空间(与之关联的概念是特征值和特征向量)的理论。
学科编码:1102110,隶属于代数学
群
论
group theory
群论是研究一种基本的代数结构——群的学科,作为一门抽象化的数学学科,群论侧重于不同群结构之间的联系和群的分类以及存在性的讨论,前者有群同态的观点,后者引出了群分类问题。近年来对比群性质稍微差一些的代数结构——半群的研究十分热门,半群论也有成为一门新学科的趋势。
学科编码:1102115,隶属于代数学
环
论
ring theory
环论是研究比群结构较为丰富的一种代数结构——环的学科,对环的研究有像群那样的性质,但环论主要侧重于两种运算诱导的新性质,如环是否是有限生成的,是否是可因式分解的等等。
学科编码:1102140,隶属于代数学
射
影几何学
projective geometry
射影几何学
学科编码:1102740,隶属于几何学
主要
页面
页面
微
分几何学
differential geometry
微分几何学
学科编码:1102745,隶属于几何学
主要
页面
页面
数
值代数
numerical algebra
数值代数
学科编码:1106150,隶属于计算数学
主要
页面
页面
概
率分布
probability distribution
概率分布
学科编码:1106420,隶属于概率论
主要
页面
页面
数
理统计学
mathematical statistics
数理统计学
学科编码:11067,隶属于数理统计学
主要
页面
页面
搜索
主页 分析 代数 几何 图片
教育水平话题
- 2022-09-15 2022高教社杯全国大学生数学建模竞赛赛题公布。
- 2022-08-23 第十三届丘成桐大学生数学竞赛圆满落幕。
- 2022-07-08 中国第十四届全国大学生数学竞赛将由广东工业大学和广东省数学会联合承办。
数学工具
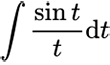
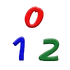



















![{\displaystyle {\dfrac {\mathbb {R} [x]}{(x^{2}+1)}}\cong \mathbb {C} }](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/ef36a404e5034486cf24460acff1e02a374485e3)