Биекция

Биекция - это взаимно однозначное отображение одного множество в другое.

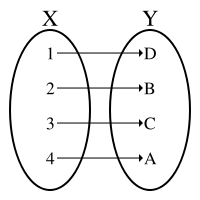
Биективная функция.

Определение

Отображение $f: X \to Y$ называется биективным (или биекцией), если оно инъективно и сюръективно.

Замечание

Два множества, между которыми существует биекция, называются равномощными.

Свойства

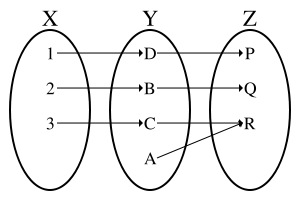
Композиция инъекции и сюръекции, дающая биекцию.

• Отображение $f: X \to Y$ является биективным тогда и только тогда, когда существует обратное отображение $f^{-1}: Y \to X$ такое, что

$f\circ f^{-1}=\operatorname {id} _{Y},\;f^{-1}\circ f=\operatorname {id} _{X},$

где $\operatorname {id}$ обозначает тождественное отображение, а $\circ$ композицию функций.

• Пусть даны два отображения $f: X \to Y$ и $g:Y\to Z,$ а $h=g\circ f:X\to Z$ - их композиция. Тогда $h$ биективно тогда и только тогда, когда $f$ инъективно, а $g$ сюръективно.
• В частности, композиция двух биективных отображений сама биективна. Обратное, вообще говоря, неверно.

Примеры

• $\operatorname {id} :X\rightarrow X$ — функция, сохраняющая все элементы множества $X$, биективна на этом множестве.
• $f(x)=x,\ f(x)=x^{3}$ — биективные функции из $\R$ в себя. Вообще, любой одночлен одной переменной нечётной степени является биекцией.
• $f(x) = e^x \!$ — биективная функция $\R$ в $\mathbb {R} _{+}=(0,\infty )$. Но если её рассматривать как функцию в $\R$, то она уже не будет биективной (у отрицательных чисел не будет прообразов).
• $f(x)= \sin x \!$ не является биективной функцией, если считать её определённой на всём $\R$.

См. также

• Инъекция;
• Сюръекция;
• Изоморфизм.

Литература

• Н. К. Верещагин, А.Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств.

• Ершов Ю. Л., Палютин Е. А. Математическая логика: Учебное пособие. — 3-е, стереотип. изд. — СПб.: «Лань», 2004—336 с.

Эта статья содержит материал из статьи Биекция русской Википедии.